Developing a Terraced Terrain Generator
In this blog post I will discuss some technical details and give a glimpse of Terraced Terrain Generator’s (TTG) development process. TTG is a free Unity tool for procedural generation of terraced terrain meshes. It’s open source and it’s on GitHub! Here are some examples of the type of terrains TTG is able to generate:

This post is part of a series that documents the development process of TTG, containing the following posts:
- Developing a Terraced Terrain Generator (this post)
- Terraced Terrain Generator performance improvements
- Adding custom terrace heights to Terraced Terrain Generator
- Adding more detail to Terraced Terrain Generator using Perlin noise octaves
The sections below follow TTG’s four terrain generation steps: basic shape generation, mesh fragmentation, mesh sculpting and terrain slicing. Then, we discuss performance improvements, additions since TTG’s first version, and future developments. Finally, a short conclusion wraps the post up.
Let’s dive in TTG’s generation steps right away.
Step 1: Basic shape generation 📐
This step is responsible for generating the polygon that will server as a basic shape for the terrain. In order words, how the terrain will look like from a high up, top view.
Supported shapes
- Equilateral triangle.
- Any regular (equilateral and equiangular) polygon, from 4 to 10 sides.
Equilateral triangle
Generating an equilateral triangle is trivial: create 3 vertices equally distant from the center of the terrain. Each pair forms a 60° angle with the center.
Any regular polygon
All other regular polygons (independent of the number of sides) will be generated using the same strategy. We take advantage of the fact that regular polygons can be created by composing triangles and define all polygon generation based on it. Regular polygons are perfect for this task because their vertices are equidistant from the polygon’s center.
💡 Although it is possible to generate polygons with any number of sides using this strategy, the number of sides is limited to 10.
Square
A square can be created by overlapping 2 isosceles, right-angled triangles on their hypotenuses. The triangles are created in a similar manner to the equilateral triangles described above, but vertices are recycled to save memory. A square contains 4 vertices and 2 triangles.
Pentagon
A pentagon can also be created using triangles, but differently from the strategies described above. A vertex is placed on the center of the pentagon and it’s used by all triangles that compose the polygon. All other vertices are equidistant from the center vertex. Once again, vertices are recycled to save memory.
Other regular polygons
Other regular polygons with more than 5 sides are created using the same strategy as the pentagon’s, just increasing the number of vertices. For example, here’s a decagon:

Step 2: Mesh fragmentation 🧨
The basic shape generated by the previous step does not contain enough vertices and triangles to generate a nice terrain. We need to fragment it into smaller triangles to increase its detail and resolution.
We start by taking advantage that all shapes generated in the previous steps are composed by triangles. Then, we can fragment these triangles into smaller ones. Breaking down a triangle into smaller triangles is trivial: divide it into 4 triangles like the image below. The outer, bigger triangle is the original one and the smaller, inner triangles are the outcome of a triangle fragmentation.
The fragmentation can continue recursively, on the generated triangles. If we fragment the 4 triangles above, we would obtain the following 16 triangles.
The more fragmentation iterations we perform, the higher is the resolution of the final mesh. We can say a mesh was fragmented with a depth D of there were performed D fragmentation iterations on it. The resulting mesh will contain $T * 4^D$ triangles, where T is the number of triangles in the original mesh and D is the fragmentation depth.
Here’s an example of a triangle that has been fragmented 6 times (depth = 6):

Here’s a pentagon that has been fragmented 5 times (depth = 5):

Step 3: Hills and valleys generation (a.k.a. mesh sculpting) 🏔
Now that we’ve got a flat surface which serves as a base to a terrain, it’s time to create hills and valleys to make the terrain more interesting.
Requirements
- Fully automate this task, eliminating the tedious job of terrain shaping.
- It should be able to repeatedly generate random terrains.
- At the same time it should have a deterministic behavior, so it could easily reproduce a given terrain whenever necessary.
- The following should be generation parameters:
- The feature frequency (how often hills and valleys are formed).
- The maximum height of the generated hills.
- The height distribution curve.
The strategy
The chosen strategy is well known in the field, yet it’s quite efficient: noise filters. These filters can generate noise, often following some pattern. Simply put, they are functions that, for a given point in space, will return a noise value - often between 0 and 1. The idea is to use the noise values to sculpt the mesh by moving its vertexes upwards, creating hills. This can be accomplished by multiplying the noise value by the maximum height, and adding it to the vertex’s y coordinate.
1
vertex.y += noise(vertex.x, vertex.y) * maximumHeight
The challenge is to choose the right filter. Fortunately, the Perlin filter is famous for delivering filters that are a great fit for the kind of sculpting we’re looking for. Better yet, Unity’s standard API already contains a function for Perlin noise: Mathf.PerlinNoise. Here’s an example of an image of a Perlin filter:

In order to control the frequency, we simply multiply the vertex coordinates by a given parameter frequency.
1
2
3
var filterX = vertex.x * frequency;
var filterY = vertex.z * frequency;
vertex.y += height * Mathf.PerlinNoise(filterX, filterY);
Unity’s API call doesn’t support randomizer seeds, so we had to get creative. We introduced randomisation by offsetting all vertices’ position by a random value.
1
2
3
4
5
6
7
8
9
10
11
12
var vertices = mesh.vertices;
var xOffset = _random.Next(-1_000, 1_000);
var yOffset = _random.Next(-1_000, 1_000);
for (var i = 0; i < vertices.Length; i++)
{
var vertex = vertices[i];
var filterX = (vertex.x + xOffset) * frequency;
var filterY = (vertex.z + yOffset) * frequency;
vertex.y += height * Mathf.PerlinNoise(filterX, filterY);
vertices[i] = vertex;
}
And to add replicable, deterministic terrain generation, the randomizer’s seed can be provided.
Outcome
The outcome was quite convincing. Here’s an example of a pentagon-based terrain, fragmented 2 times (depth = 2), with a maximum height of 5 and a frequency of 0.2.

Here’s another example; an octagon-based terrain, fragmented 6 times (depth = 6), with a maximum height of 10 and a frequency of 0.2.

Here’s the same octagon-based terrain with a frequency of 0.5:

Height curve
Even though this strategy delivers great results and we can control the noise frequency, it would be great if we could control other parameters. For example, we could benefit from controlling the height distribution over the terrain: how low valleys and how high hills should be, and everything in between. This would allow developers to customize the terrain with characteristics such as “I want a mostly flat terrain, with sudden hills”.
This can be accomplished by using a height curve that modifies the output of the Perlin noise algorithm. This curve would be limited to the [0,1] interval, on both X and Y axes, where the X axis represents the Perlin noise output and the Y axis represents the modified value. Finally, the final value can be multiplied by the maximum height as explained on the section above.
Such a curve can be easily defined in Unity using Animation Curves. The function that calculates the height of a given points becomes:
1
2
3
4
5
6
7
8
9
static float GetHeight(float x, float y, float maximum, AnimationCurve heightDistribution)
{
// Step 1, fetch the noise value at the given point
var noise = Mathf.PerlinNoise(x, y);
// Step 2, apply the height sculpting curve (if it's not null) to the noise value
var modifier = heightDistribution?.Evaluate(noise) ?? 1;
// Step 3, apply the modifier to the maximum height
return maximum * modifier;
}
At this point, we can start playing with the height distribution curve. Let’s play with a given terrain, changing the height distribution curve to see how it modified the generated terrain. A “neutral” curve (a curve that doesn’t modify the Perlin noise values) should output the same value as its input. That can be accomplished with a linear curve starting from (0,0) and ending at (1,1).
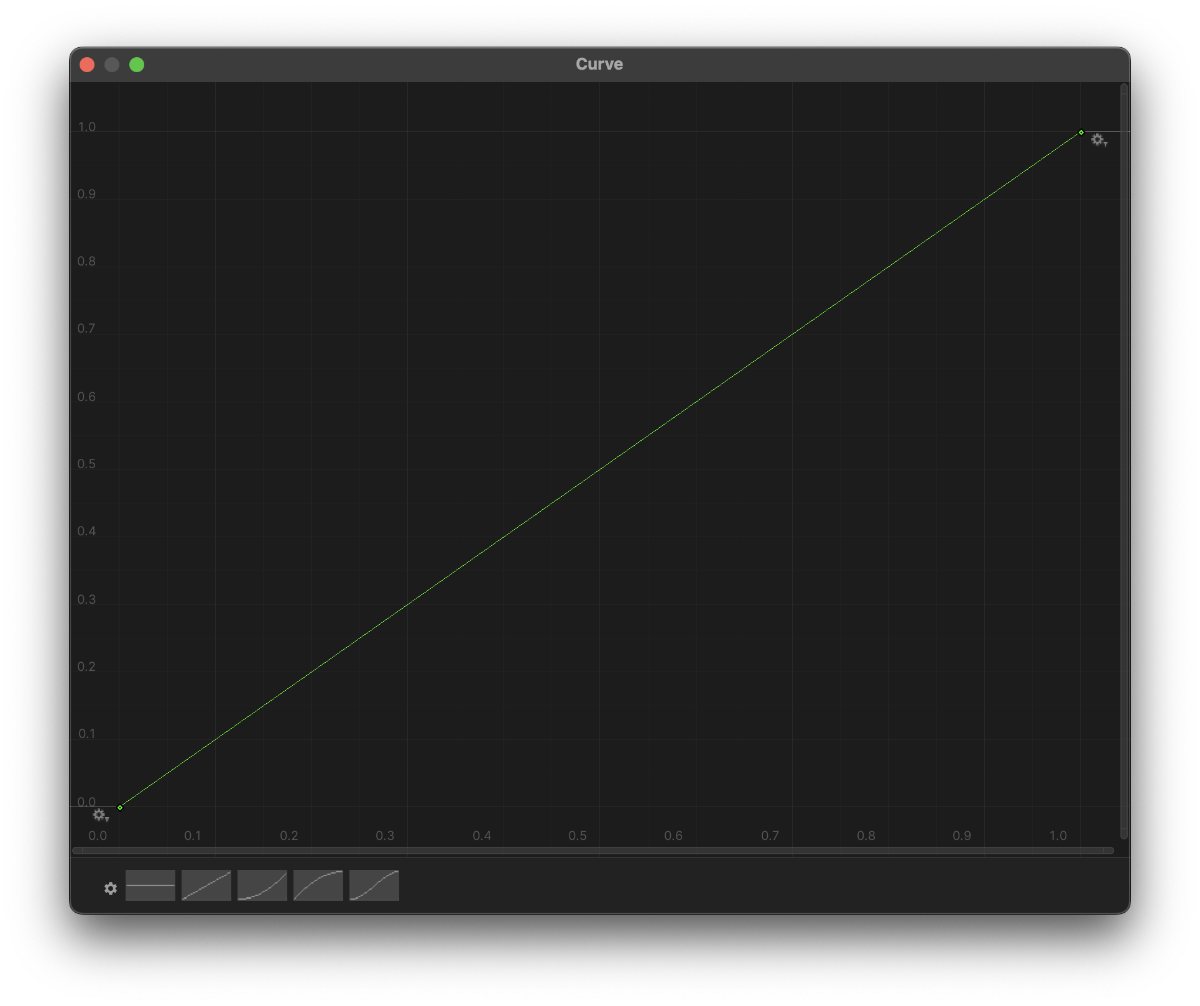
The neutral curve generates the following unmodified terrain:

Now let’s start playing with the height distribution curve. First, let’s try to change it to the following exponential curve:
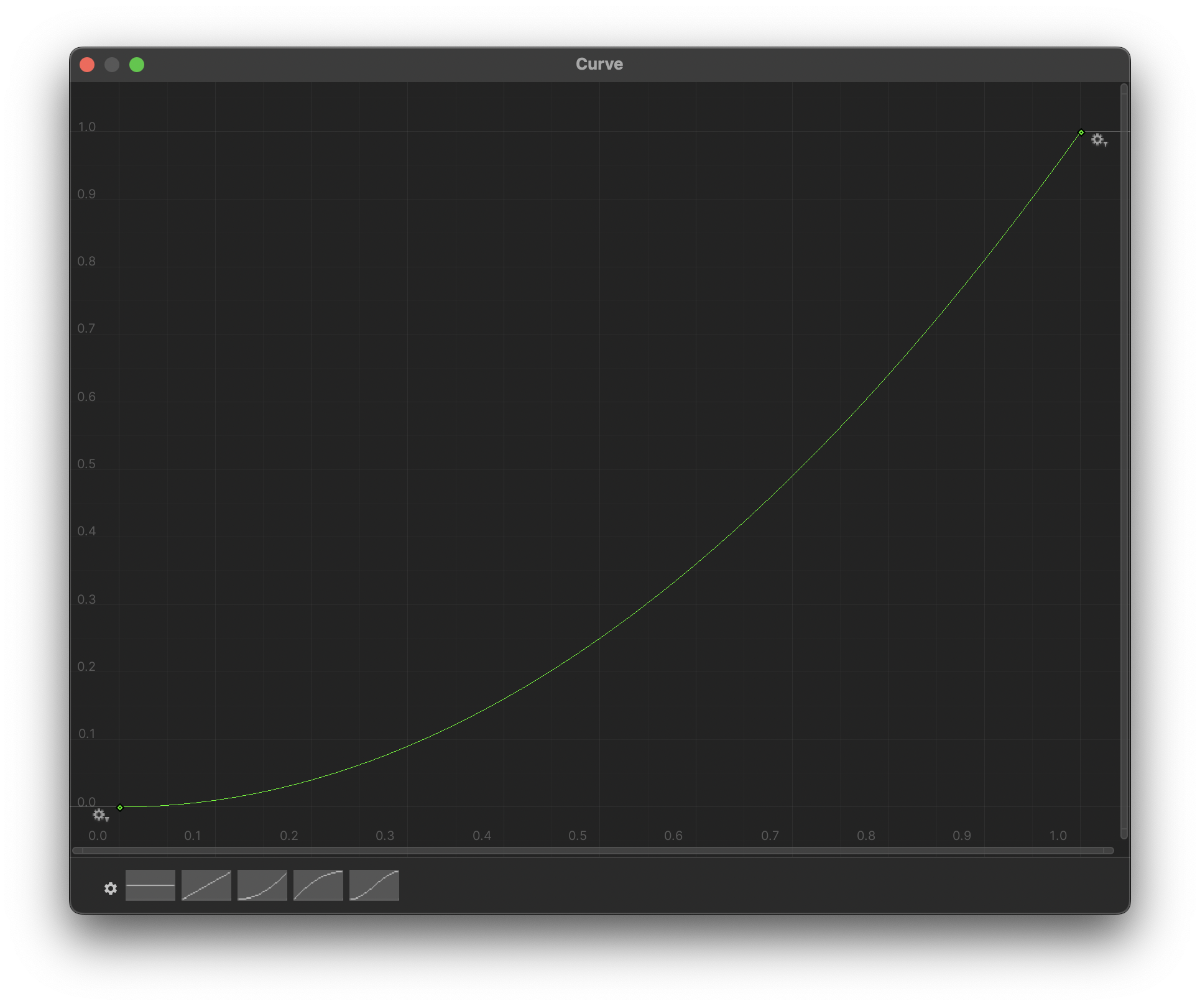
The curve above generates the terrain below. Notice how the hills seem higher. In reality, they are not; the valleys around the hills are lower.

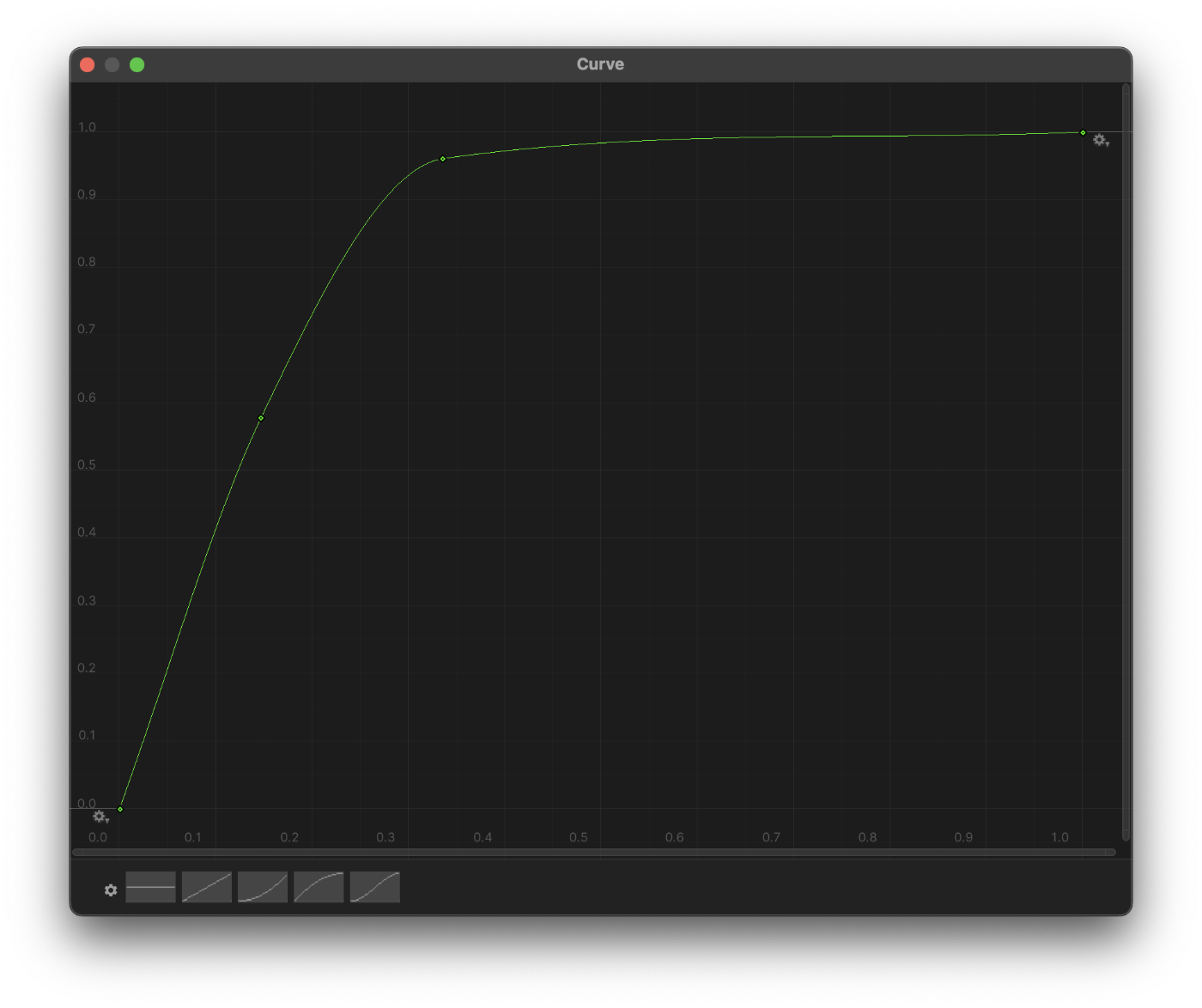
Let’s be even more aggressive in that distribution, bringing the lower values even closer to the Y=0 line and rise quickly towards (1,1):
The curve above generates the following terrain. As expected, the terrain is flatter and the hills quickly “bump” out of the plane.

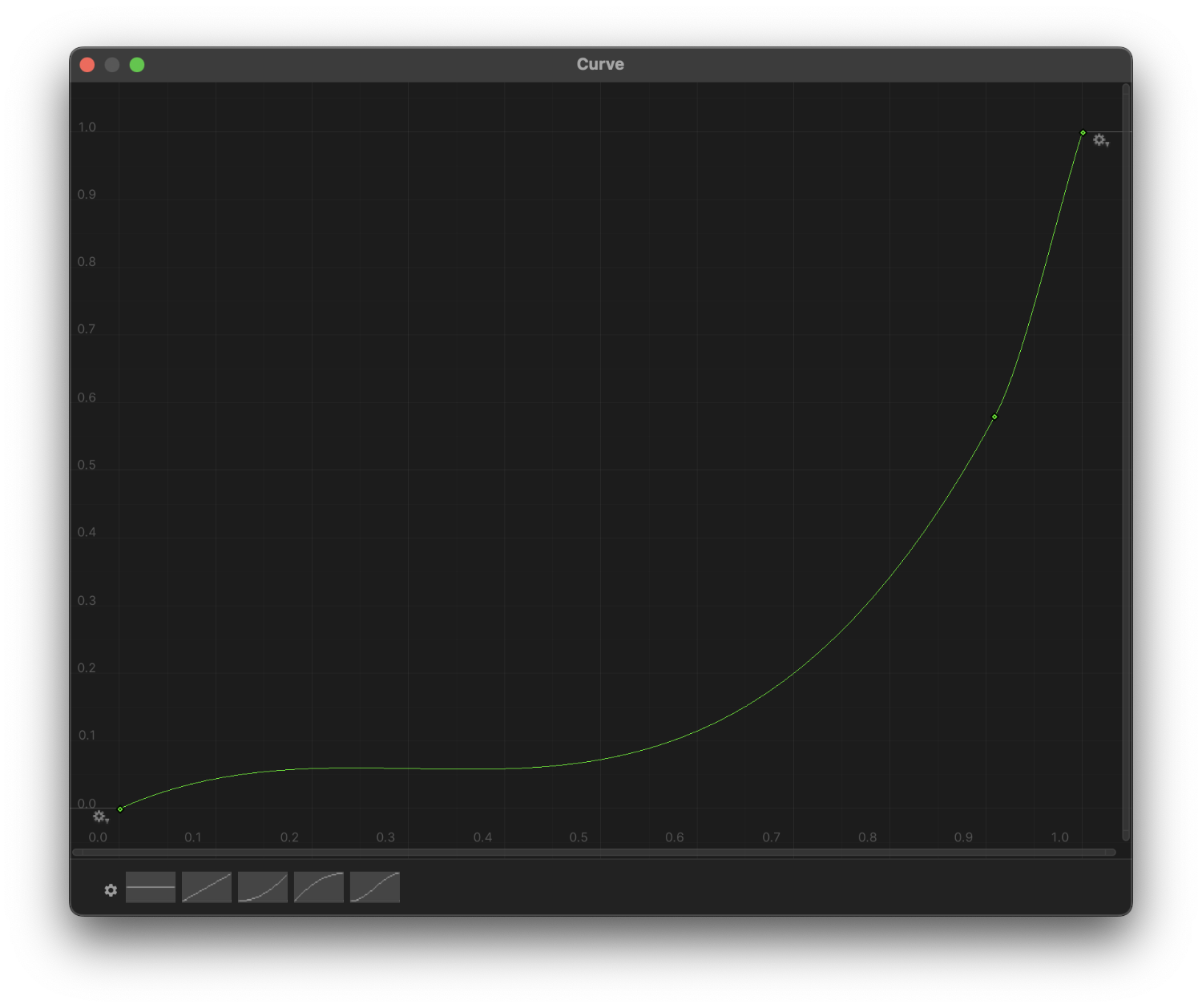
We can get more creative and create curves like the one below, which creates a plateau with a few canyons:
The curve above generates the terrain below.

Or even a curve that has a plateau, but still has both hills and valleys:
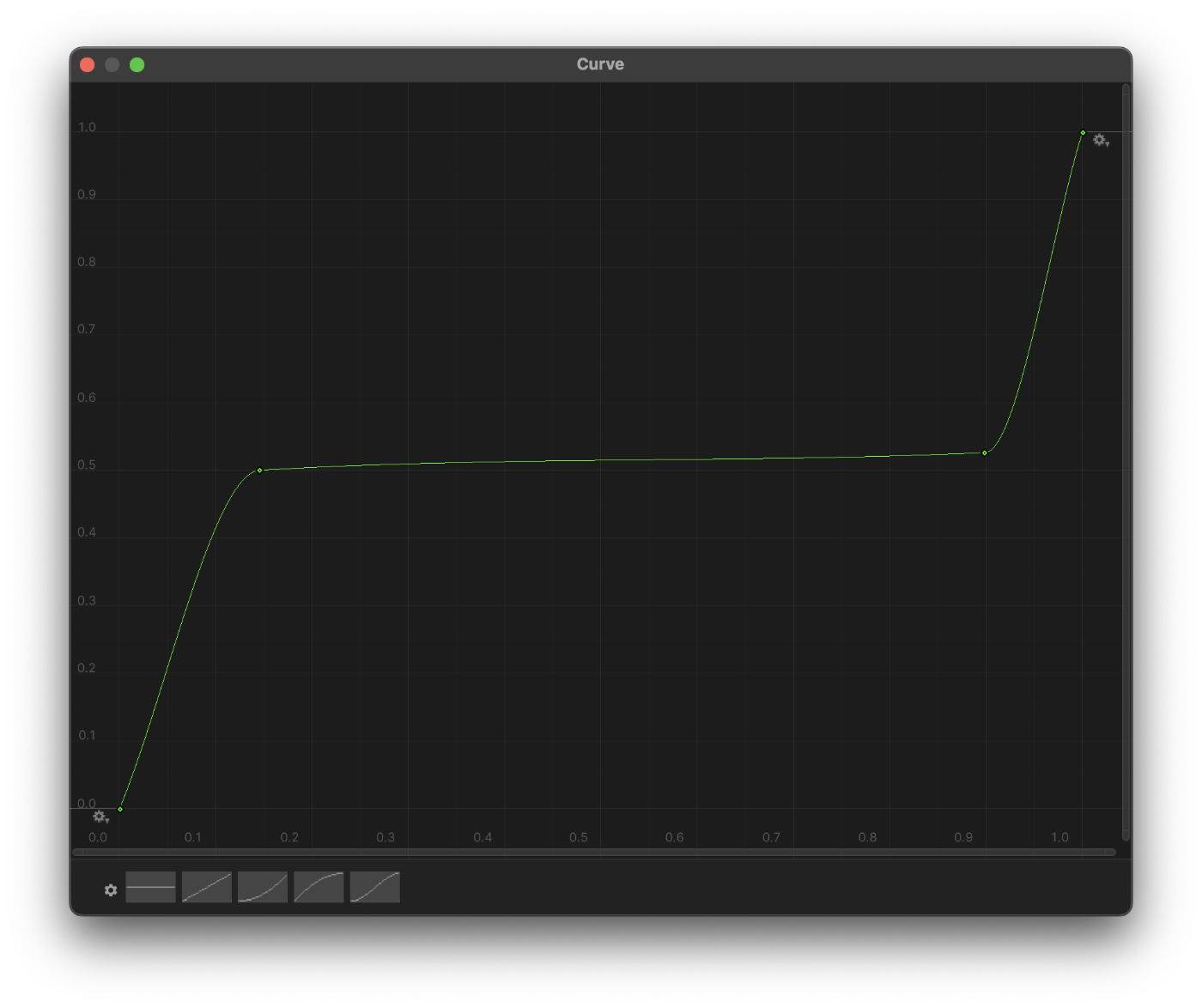
The curve above generates the terrain below.

At this point, we have good control of the height distribution.
Step 4: Terrain slicing 🔪
The approach
Now that we’ve got a terrain with hills and valleys, it’s time to start creating some terraces. the method I used was based on Icospheric Planetoid’s approach of using the meandering triangles algorithm to slice each triangle using planes that are located exactly where the terraces will be. Check their article for further explanation on how that algorithm can be applied on this domain.
Here’s an example of a terrain before and after slicing it into 15 terrains:


The end result looks great, but something is missing…
Material assignment
Using the same material for all terraces is boring. Ideally, we should be able to assign a different material for each terrace to introduce some color palettes and progressions. To achieve this, terrace generation creates multiple sub-meshes, one for each terrace. This simple trick allows for material assignment on a sub-mesh basis in Unity. The image below is an example of how simple color changes can influence a terrain’s look:

Performance improvements ⚡️
Even though the goal of the terraced terrain generator was mostly accomplished on the feature level, performance was far from ideal. The efforts put into performance improvements were described in a separate article.
Additions ✅
The features discussed up to this point shipped on TTG 1.0.0. The following features expanded TTG’s capabilities and shipped on later releases:
- Custom terrain heights: instead of evenly spacing the terraces between the terrain’s lowest and highest points, allow custom heights to be chosen. This feature was implemented on version 1.1.0 and it’s detailed on its own blog post.
- Improved terrain detailing: use Perlin noise octaves to create more natural terrains. This feature was implemented on version 1.2.0 and it’s described on its own blog post.
These additions enabled a new level of expressiveness and detailing on TTG terrains. The image below displays example terrains that were generated using TTG 1.2.0:

What’s next? 🔮
Although it looks like the Terraced Terrain Generator is complete, there’s always more work to be done. The following features are planned in future updates:
- Sphere as a basic shape: let’s create completely terraced planets!
- Realtime sculpting: instead of letting an algorithm generate the hills, let the user interactively sculpt them.
- Outer walls: “close” the generated mesh so it looks like a model carved in wood, sitting on a desk.
You can follow the development of TTG in its Trello board. If you have suggestions, feature requests or bugs to report, use the Issues section of TTG’s GitHub repository to communicate them.
Conclusion 🏁
TTG was a great side project that taught me a lot about several aspects of game development tools creation—including non-coding nuances. I hope the effort I’ve put in the creation of the tool and its documentation help someone out there.
If you made it this far, thank you very much for the dedication. I hope you’ve found this an interesting read. As usual, feel free to leave comments, suggestions or corrections in the comments section. See you next time!




